【jdb电子游戏平台网站
网】〈接上期——〉
五、夹角γ为75°的计算
5.1用基础理论分析图7形式顺时针转动时惯性力


①一阶惯性力的计算
一阶惯性力用  表示,下标
表示,下标  代表一阶。按照图7从左到右的阅读顺序,其一阶惯性力合力的构成如(7)式所表达
代表一阶。按照图7从左到右的阅读顺序,其一阶惯性力合力的构成如(7)式所表达














坐标系如图顺转15°后,由于y轴在标准直角坐标的对面,相当于坐标系逆时针旋转15°,也就
是作正角15°变换,其因子为,
则

②二阶惯性力的计算
这里先用传统的三角函数来计算。
垂直方向:


先积化和差,得到






展开化简合并后得到


水平方向:
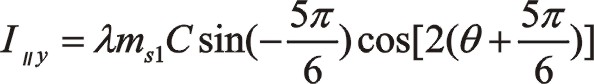

这里应注意投影到y轴应为负值,这也和前面的正方向原则相一致。否则影响到转换矩阵,影响到诸如式(34)等的形式。



也可以采用复数分析法,下面简单地写出。二阶惯性力用  表示,下标
表示,下标  代表二阶。按照图7从左到右的阅读顺序,其二阶惯性力合力的构成如(11)式所表达
代表二阶。按照图7从左到右的阅读顺序,其二阶惯性力合力的构成如(11)式所表达





关于W型75°顺转二阶惯性力也可以类似一阶惯性力作其逆矩阵(见下)求出其二次多项式,判定其椭圆,此处不展开了;也可以作正角15°矩阵变换,求出其关于转角的参数方程,得出的结果太复杂,这里写出其线性方程,读者有兴趣可以验算一下四个涉及到三个无理数的方程运算。



5.2用基础理论分析图8形式反时针转动时惯性力

①一阶惯性力的计算
同样,一阶惯性力合力的构成按图8所示的构成,依次写出如下













由上式可以发现,将式(34)中的“θ”用“-θ”,“Y”用“-Y”代替后就得出上面的式子。这也就是转角换向就用负角代替,按基础理论中正方向的问题所要求的,依图7中所建立的坐标系,由于y轴较前一种方向相反,所以y轴也要变号。

经求上矩阵的逆矩阵得:

该逆矩阵是这样求得的,令, 则原矩阵为
则原矩阵为 ,先求其行列式的值,用含有字母a的代数式表示,上矩阵的伴随阵是
,先求其行列式的值,用含有字母a的代数式表示,上矩阵的伴随阵是 ,依据
,依据 ,矩阵的四项将a值代入,计算化简后得出含有根号的分式。
,矩阵的四项将a值代入,计算化简后得出含有根号的分式。
利用cos2θ+sin2θ=1,求出关于X、Y的二次多项式,利用其判别式定理,求得AC=0.238≠0,B2-4AC=-0.893<0。所以其一阶惯性力图是一个椭圆。
坐标系作负角15°变换,则



故其一阶惯性力图是一个椭圆。
②二阶惯性力的计算
二阶惯性力合力的构成按图8所示的构成,依次写出如下










关于它是一个椭圆,类同以上。读者有兴趣也可仿上步骤算出这个矩阵。上式与式(42)相类似,读者应明白其构成。
5.3用基础理论分析图9形式顺时针转动时惯性力

①一阶惯性力的计算




根据式(50)、(46)、(35),依上一篇文章的内容,可以得出W型75°jdb电子游戏平台网站
上述三种情形一阶惯性力的椭圆的短长轴之比为 。
。
②二阶惯性力的计算
这里也先用传统的三角函数来计算。
垂直方向:


先和差化积,得到


水平方向:



如用复数分析法,则如上结果相同。
根据式(53),依上一篇文章的内容,可以得出W型75°jdb电子游戏平台网站
上述三种情形二阶惯性力的椭圆的短长轴之比为 。
。
5.4总结
本处以安徽华晶机械有限公司生产的WW-0.9/10B-Q型全无油二级空压机为模版,假定气缸夹角为75°,计算其一、二阶往复惯性力。此处先假定三列往复质量相等,即ms为1.8kg,曲柄半径为0.0375m,曲柄半径连杆比λ为37.5/195,角速度ω为2π×(800/60)rad/s,现将上述结构参数分别代入上文中所列的相关公式中,运用计算机内EXCEL程序列表、绘图计算分析,计算的结果绘制在上图的图7、图8、图9中,可以得到以下结论:
1)一阶惯性力由60°分布的圆变成椭圆,且椭圆的短长轴之比由1变成0.608;平均值由711N变成721N,有所增大;方向由跟随变成近似跟随。图7、8中已画出一、二阶惯性力刚开始时的矢量线,用椭圆断开表示,图9中反映一阶惯性力在某个时候有重合的可能。
2)二阶力说明,其椭圆短长轴之比由0.333变成0.571。力的平均值由96.9N变成70.4N,有所减小。方向初看是乱的,但很有规律,因为三角函数是周期函数。这个规律待人们去认识、研究、发现、找寻合适的机构来平衡。
3)当ms2≠ms1时,60°分布一阶惯性力在ms2列方向形成椭圆的对称轴,而75°不是,说明角度优先于质量,说明W型时,60°分布是最优的。从式(9)的复数表达式、式(10)的几何表达式中可以看出,60°分布时一阶惯性力长短轴与角度无关,仅与质量有关,这与上也是吻合的。
4)它们的共同点是,曲柄转1周,一阶惯性力也转1周,且同向;二阶惯性力转2周,也同向。
5)若ms2≠ms1,会引起图7、图8、图9中两个椭圆有所歧化,或偏转,兼带扩压,使其相位、幅值有微量变化。
5.5 图9与图7中隐含的一致性方程
我们将图9中坐标系顺旋转方向转动75°后建立了新坐标系,就变成了图7中坐标系,这也是正角变换,我们可以得出这两个代数式方程(50)、(34)之间的相互联系,用下面的矩阵方程来表达,以验算一阶惯性力理论推导过程的一致性。


〈注:本文未完待续,更多精彩见下期!〉
参考文献
(1)宋瑞林,气缸夹角为60°的V6车用发动机往复惯性力的平衡分析,[J],汽车技术,1988.8
(2)李松虎,3W型活塞jdb电子游戏平台网站
往复惯性力的分析,[J],jdb电子游戏平台网站
技术,1987.3
(3)陆鹏程,张光胜,三星型jdb电子游戏平台网站
振动问题研究,[J],安徽工程科技学院学报,2009.1
(4)王再顺,夹角为90°的V型jdb电子游戏平台网站
往复惯性力平衡的探讨,[J],jdb电子游戏平台网站
技术,1986.2
来源:本站原创
【jdb电子游戏平台网站 网】〈接上期——〉
五、夹角γ为75°的计算
5.1用基础理论分析图7形式顺时针转动时惯性力


①一阶惯性力的计算
一阶惯性力用  表示,下标
表示,下标  代表一阶。按照图7从左到右的阅读顺序,其一阶惯性力合力的构成如(7)式所表达
代表一阶。按照图7从左到右的阅读顺序,其一阶惯性力合力的构成如(7)式所表达

![]()












坐标系如图顺转15°后,由于y轴在标准直角坐标的对面,相当于坐标系逆时针旋转15°,也就
是作正角15°变换,其因子为,
则

②二阶惯性力的计算
这里先用传统的三角函数来计算。
垂直方向:


先积化和差,得到






展开化简合并后得到


水平方向:
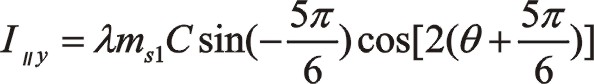

这里应注意投影到y轴应为负值,这也和前面的正方向原则相一致。否则影响到转换矩阵,影响到诸如式(34)等的形式。



也可以采用复数分析法,下面简单地写出。二阶惯性力用 ![]() 表示,下标
表示,下标 ![]() 代表二阶。按照图7从左到右的阅读顺序,其二阶惯性力合力的构成如(11)式所表达
代表二阶。按照图7从左到右的阅读顺序,其二阶惯性力合力的构成如(11)式所表达





关于W型75°顺转二阶惯性力也可以类似一阶惯性力作其逆矩阵(见下)求出其二次多项式,判定其椭圆,此处不展开了;也可以作正角15°矩阵变换,求出其关于转角的参数方程,得出的结果太复杂,这里写出其线性方程,读者有兴趣可以验算一下四个涉及到三个无理数的方程运算。



5.2用基础理论分析图8形式反时针转动时惯性力

①一阶惯性力的计算
同样,一阶惯性力合力的构成按图8所示的构成,依次写出如下













由上式可以发现,将式(34)中的“θ”用“-θ”,“Y”用“-Y”代替后就得出上面的式子。这也就是转角换向就用负角代替,按基础理论中正方向的问题所要求的,依图7中所建立的坐标系,由于y轴较前一种方向相反,所以y轴也要变号。

经求上矩阵的逆矩阵得:

该逆矩阵是这样求得的,令, 则原矩阵为
则原矩阵为 ,先求其行列式的值,用含有字母a的代数式表示,上矩阵的伴随阵是
,先求其行列式的值,用含有字母a的代数式表示,上矩阵的伴随阵是![]() ,依据
,依据![]() ,矩阵的四项将a值代入,计算化简后得出含有根号的分式。
,矩阵的四项将a值代入,计算化简后得出含有根号的分式。
利用cos2θ+sin2θ=1,求出关于X、Y的二次多项式,利用其判别式定理,求得AC=0.238≠0,B2-4AC=-0.893<0。所以其一阶惯性力图是一个椭圆。
坐标系作负角15°变换,则



故其一阶惯性力图是一个椭圆。
②二阶惯性力的计算
二阶惯性力合力的构成按图8所示的构成,依次写出如下










关于它是一个椭圆,类同以上。读者有兴趣也可仿上步骤算出这个矩阵。上式与式(42)相类似,读者应明白其构成。
5.3用基础理论分析图9形式顺时针转动时惯性力

①一阶惯性力的计算




根据式(50)、(46)、(35),依上一篇文章的内容,可以得出W型75°jdb电子游戏平台网站
上述三种情形一阶惯性力的椭圆的短长轴之比为![]() 。
。
②二阶惯性力的计算
这里也先用传统的三角函数来计算。
垂直方向:


先和差化积,得到


水平方向:



如用复数分析法,则如上结果相同。
根据式(53),依上一篇文章的内容,可以得出W型75°jdb电子游戏平台网站
上述三种情形二阶惯性力的椭圆的短长轴之比为 。
。
5.4总结
本处以安徽华晶机械有限公司生产的WW-0.9/10B-Q型全无油二级空压机为模版,假定气缸夹角为75°,计算其一、二阶往复惯性力。此处先假定三列往复质量相等,即ms为1.8kg,曲柄半径为0.0375m,曲柄半径连杆比λ为37.5/195,角速度ω为2π×(800/60)rad/s,现将上述结构参数分别代入上文中所列的相关公式中,运用计算机内EXCEL程序列表、绘图计算分析,计算的结果绘制在上图的图7、图8、图9中,可以得到以下结论:
1)一阶惯性力由60°分布的圆变成椭圆,且椭圆的短长轴之比由1变成0.608;平均值由711N变成721N,有所增大;方向由跟随变成近似跟随。图7、8中已画出一、二阶惯性力刚开始时的矢量线,用椭圆断开表示,图9中反映一阶惯性力在某个时候有重合的可能。
2)二阶力说明,其椭圆短长轴之比由0.333变成0.571。力的平均值由96.9N变成70.4N,有所减小。方向初看是乱的,但很有规律,因为三角函数是周期函数。这个规律待人们去认识、研究、发现、找寻合适的机构来平衡。
3)当ms2≠ms1时,60°分布一阶惯性力在ms2列方向形成椭圆的对称轴,而75°不是,说明角度优先于质量,说明W型时,60°分布是最优的。从式(9)的复数表达式、式(10)的几何表达式中可以看出,60°分布时一阶惯性力长短轴与角度无关,仅与质量有关,这与上也是吻合的。
4)它们的共同点是,曲柄转1周,一阶惯性力也转1周,且同向;二阶惯性力转2周,也同向。
5)若ms2≠ms1,会引起图7、图8、图9中两个椭圆有所歧化,或偏转,兼带扩压,使其相位、幅值有微量变化。
5.5 图9与图7中隐含的一致性方程
我们将图9中坐标系顺旋转方向转动75°后建立了新坐标系,就变成了图7中坐标系,这也是正角变换,我们可以得出这两个代数式方程(50)、(34)之间的相互联系,用下面的矩阵方程来表达,以验算一阶惯性力理论推导过程的一致性。


〈注:本文未完待续,更多精彩见下期!〉
参考文献
(1)宋瑞林,气缸夹角为60°的V6车用发动机往复惯性力的平衡分析,[J],汽车技术,1988.8
(2)李松虎,3W型活塞jdb电子游戏平台网站 往复惯性力的分析,[J],jdb电子游戏平台网站 技术,1987.3
(3)陆鹏程,张光胜,三星型jdb电子游戏平台网站 振动问题研究,[J],安徽工程科技学院学报,2009.1
(4)王再顺,夹角为90°的V型jdb电子游戏平台网站 往复惯性力平衡的探讨,[J],jdb电子游戏平台网站 技术,1986.2
来源:本站原创





网友评论
条评论
最新评论